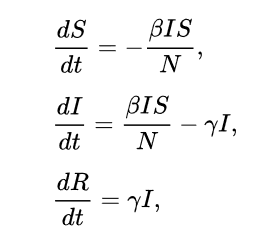I august 1954-nummeret af Astounding science fiction kunne man læse en novelle af Tom Godwin med titlen “The cold equations”. Novellen er siden blev meget diskuteret blandt science fiction-fans og -forfattere. Handlingen er kort fortalt den, at en pilot på et rumskib opdager en blind passager på sit rumskib. Han er på vej til en rumkoloni hvor en dødbringende epidemi er i gang, og hvor de har desperat brug for det serum han har i lasten. Efter at have regnet på det, finder han ud af at den blinde passager vejer så meget at hans brændstof ikke rækker til at nå frem med serummet i tide. Så han må vælge mellem de syge på kolonien og den blinde passager.
Novellen fortæller os at de kolde ligninger har afsagt en dødsdom over den blinde passager. Det er ren matematik at hun må dø. Det kan diskuteres om ikke der var måder at redde hende på, og om hvorfor der ikke er taget højde for at man kunne få brug for mere brændstof i en nødsituation. Men pointen er at der er fysiske love vi ikke kan overtræde, uanset hvor meget vi gerne vil.
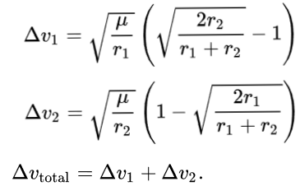
I den igangværende COVID-19 epidemi har myndighederne gjort et rigtig godt arbejde med at håndtere situationen og ikke skabe panik. Det har måske fået mange til at tro at en sådan epidemi er noget der går over lige om lidt. Men epidemier er, ligesom brændstofberegninger for rumskibe, også noget der styres af lovmæssigheder. Det kan man regne på ved hjælp af forskellige modeller. Hvor rumskibes vægt, brændstoffers brændværdi og afstande i rummet kan måles ret præcist, er det straks sværere at sætte tal på en epidemi. Men der er visse lovmæssigheder som ligger ret fast med epidemier.
En epidemi er en sygdom som spreder sig i en befolkning, så flere og flere bliver smittede over tid. Et ofte brugt tal for det er R0. Det vil sige hvor mange hver smittet person i gennemsnit selv når at smitte. Det er et tal som afhænger af rigtig mange ting, så det er ikke noget man kan beregne sig til, men noget man kan observere, ud fra hvor hurtigt sygdommen spreder sig. Hvis R0 er mindre end 1, vil sygdommen langsomt dø ud, mens et R0 på over 1 betyder at sygdommen stadig breder sig. R0 ændrer sig, hvis folks adfærd ændrer sig. Holder de fleste mennesker sig for eksempel isolerede fra andre mennesker, vil de nå at smitte færre andre mennesker, og derved sænkes R0. En anden måde epidemier bremses på, er ved at dem der allerede har haft sygdommen normalt ikke får den igen. I hvert fald ikke før epidemien slutter. Man siger at de er immune. Hvis hver smittet person kommer i kontakt med de samme antal mennesker, vil de alt andet lige smitte færre, hvis nogle af dem de er i kontakt med er immune.
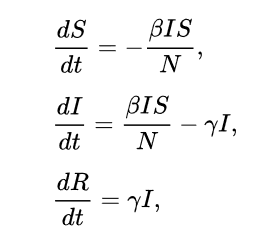
En meget brugt model for epidemier er SIR-modellen. Den bruges for eksempel af Sundhedsstyrelsen i Danmark til at regne på den igangværende COVID-19 epidemi. Med den får man et forløb af epidemien, hvor der på et tidspunkt nås et toppunkt, der hvor antallet af immune er så stort, at hver smittet person i gennemsnit smitter en anden person. Herefter vil antallet af immune vokse yderligere, til epidemien til sidst dør ud. Det tal der vises på Y-aksen for en graf over SIR-modellen kan for eksempel være antal der er syge på på et givent tidspunkt (eller som herunder: antal syge der kræver indlæggelse, som kan være en procentdel af de syge).
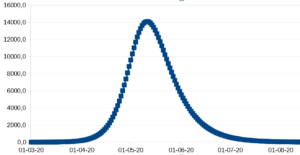
Hvis man for eksempel laver nogle foranstaltninger så mange folk holder sig hjemme, kan det tænkes at R0 sænkes til en lavere værdi. Det giver en fladere, men længere kurve. Som her, hvor toppunktet er rykket omkring en måned frem i tid, men der til gengæld kun er brug for ca. halvt så mange sengepladser på hospitalerne.
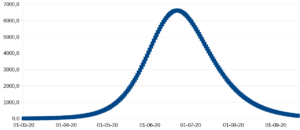
Det er så forudsat at folk stadig holder sig hjemme indtil epidemien dør ud efter nogle måneder. Hvis man på et tidspunkt vender tilbage til normal adfærd, vil kurven fortsætte med den højere værdi af R0 man startede med. I eksemplet her ophæves hjemsendelsen efter ca. en måned.
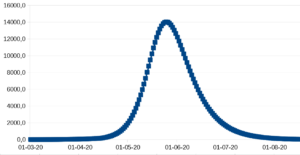
Som det ses, er vi næsten tilbage ved den første graf, med det tidlige, men høje toppunkt. Det skyldes at kun ganske få er nået at blive immune så tidligt i epidemien. Hvis man derimod venter med at lukke folk ud til lidt efter toppunktet er nået, ser det bedre ud:
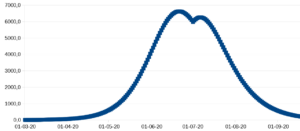
Nu kommer antal indlagte ikke højere op end da vi holdt folk inde helt til epidemien var helt ovre. Måske skulle man lige have ventet en uges tid mere, for at undgå den lille stigning der sker umiddelbart efter man lukker ud. Men det vigtigste er at antallet af nødvendige hospitalssenge er begrænset. Til gengæld skal folk holde sig inde til midt på sommeren.
Hvis man fra starten af havde spærret grænserne forholdsvis effektivt af, og opsporet samtlige smittede og dem som de havde smittet, kunne man måske have holdt virussen helt ude. Teoretisk set kan man også indføre så mange foranstaltninger at R0 bliver presset under 1 og epidemien dør hurtigt ud.
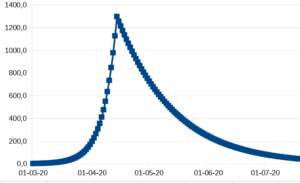
Det ser jo umiddelbart ret fantastisk ud, hvis det kan lade sig gøre. Men det vil kræve ret ekstreme foranstaltninger. Og ulempen ved det ses her:
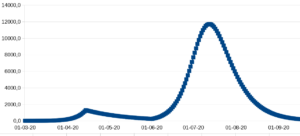
Så snart folk lukkes ud, vil epidemien køre videre for næsten fuld tryk. Med mindre man helt får udryddet virussen. Og hvis den stadig findes et sted i verden, må man opretholde overvågningen af grænser med karantæne og så videre. Når der engang kommer en vaccine, og en stor del af befolkningen er blevet vaccineret, kan der lukkes op igen, fordi smitten så ikke mere vil kunne brede sig som en epidemi.
I Godwins novelle kan man påpege mange ting piloten kunne have gjort i stedet for at smide den blinde passager ud for at dø. Tilsvarende er der også mange ting man kan gøre ved en epidemi, frem for at lade en masse mennesker dø. For eksempel kan man holde dem der er mest sårbare overfor sygdommen isoleret til epidemien er ovre. Og vigtigst måske: Sørge for at der er nok læger, sygeplejersker, respiratorer m.m. til alle de syge når epidemien er på sit højeste.

Måske er vi heldige så sygdommen er mindre farlig end de data vi har nu tyder på. Men indtil videre er disse her “kolde ligninger” det bedste bud på hvad der sker og hvad vi kan gøre ved det. Og endelig vil jeg gerne advare mod at tage mine beregninger her for noget man direkte kan bruge til at forudsige med. Jeg har slet ikke den viden og de data som Sundhedsstyrelsen og Seruminstituttet har, så hold øje med hvad de offentliggør, hvis du vil have præcise data. Jeg har bare prøvet at forklare hvordan dette her sæt kolde ligninger fungerer i forhold til COVID-19 epidemien.
Godwins novelle findes på online magasinet Lightspeeds hjemmeside.
Den findes på dansk i Science Fiction Cirklens antologi “Den Store Science Fiction-bog“.
Sundhedsstyrelsens analyser opdateres jævnligt her under epidemien.